'Attention? Attention!' 则是更详细地介绍了 Attention 的不同种类和用途。Attention 的关键在于使用 alignment score 从 input 中提取 context vector 作为辅助信息,所以不同的 alignment score 计算方式也就诞生了不同的 attention 类型:
1. self-attention: 每一个输入都和之前的输入计算相关性
2. global/soft attention: 每一个输出都和所有输入计算相关性
3. local/hard attention: 先计算一个输入范围,然后输出只和这个范围内的输入计算相关性
以前介绍过实现 GPT 的 transformer 是用 multi-head attention heads 完全取代 RNN 实现了 seq2seq 的功能。文中还介绍了 attention 的其他一些应用,比如在 Pointer Network 中,让 decoder 可以利用 attention 选择下一轮迭代的 encoder,从而实现让神经网络可以循环迭代解决 irreducible computation 问题。
https://youtu.be/2d8j_q2tl9c?si=qcFxhjBXkmJ2IKo1
FT 关于拼多多的报道,非常有趣。
你粗略看去,拼多多/TEMU 正在疯狂地抢占市场,其商品和广告在身边无处不在,其美国公司也在 NASDAQ 上市,看上去似乎一切都很正常。
但是随着 FT 的财经记者深入挖掘,就会发现拼多多和你所以为的“上市公司”完全不一样,这公司的中国公司起源于一家法人为一名老太的皮包公司,而其在美国上市的公司则是一家注册在开曼群岛的公司,这家公司的股权结构和公开信息都一塌糊涂,名义上和中国的拼多多实际上根本没任何关系,毕竟拼多多根本没有在香港上市,也并不是人们过去所熟悉的 VIE 结构。简而言之,美股的拼多多根本就是一家空壳,FT 的记者发出了灵魂拷问:请问在美股上购买拼多多的人,究竟在买什么?
最近 PDD 还告知美国 SEC 其将总部搬到了爱尔兰,但其爱尔兰办公室实际上只是一个空壳办公处,在该地址注册的是一家名为 WhaleCo 的公司,PDD 声称 WhaleCo 是自己的全资子公司,负责其全球拓展业务。
TEMU 也是疑云重重,它的起源故事一再更换,最新的版本是这是一家 2022 年成立于波士顿的“本土企业”。TEMU 的低价来于美国对低价邮包的免税政策,而对该政策的滥用显然会引起地缘政治冲突。
此外还介绍了 PDD 的商业模式,通过 Factory to Consumer (F2C) 的模式,PDD 提供市场营销、广告、设计等环节,让企业直接给终端消费者发货,同时给企业提供市场反馈和进一步的改进建议,大部分建议都是放弃一部分的品质换取大幅降价。简而言之,通过放弃品牌,从而大幅压缩成本,最终构成了 PDD 的极致低价。但是其品质往往非常低劣,一些消费者也表示不会从 PDD 购买重要的商品。
FT 关于拼多多的报道,非常有趣。
你粗略看去,拼多多/TEMU 正在疯狂地抢占市场,其商品和广告在身边无处不在,其美国公司也在 NASDAQ 上市,看上去似乎一切都很正常。
但是随着 FT 的财经记者深入挖掘,就会发现拼多多和你所以为的“上市公司”完全不一样,这公司的中国公司起源于一家法人为一名老太的皮包公司,而其在美国上市的公司则是一家注册在开曼群岛的公司,这家公司的股权结构和公开信息都一塌糊涂,名义上和中国的拼多多实际上根本没任何关系,毕竟拼多多根本没有在香港上市,也并不是人们过去所熟悉的 VIE 结构。简而言之,美股的拼多多根本就是一家空壳,FT 的记者发出了灵魂拷问:请问在美股上购买拼多多的人,究竟在买什么?
最近 PDD 还告知美国 SEC 其将总部搬到了爱尔兰,但其爱尔兰办公室实际上只是一个空壳办公处,在该地址注册的是一家名为 WhaleCo 的公司,PDD 声称 WhaleCo 是自己的全资子公司,负责其全球拓展业务。
TEMU 也是疑云重重,它的起源故事一再更换,最新的版本是这是一家 2022 年成立于波士顿的“本土企业”。TEMU 的低价来于美国对低价邮包的免税政策,而对该政策的滥用显然会引起地缘政治冲突。
此外还介绍了 PDD 的商业模式,通过 Factory to Consumer (F2C) 的模式,PDD 提供市场营销、广告、设计等环节,让企业直接给终端消费者发货,同时给企业提供市场反馈和进一步的改进建议,大部分建议都是放弃一部分的品质换取大幅降价。简而言之,通过放弃品牌,从而大幅压缩成本,最终构成了 PDD 的极致低价。但是其品质往往非常低劣,一些消费者也表示不会从 PDD 购买重要的商品。
有人问了关于签发 CRLs 的问题,正好查了些资料。
简而言之,CRLs 是一个证书列表,用来列举已经被吊销的证书。证书中有个属性叫做 CRL Distribution Points,用来指定对应 CRLs 的下载地址。
每个 CRLs 都有一个 scope,即定义它所管辖的证书。一般来说,CRLs 应该由某个 CA 来签发,这个 CA 称为它的 issuer,而这个 CRLs 的 scope 就是这个 issuer 所签发的其他证书。
但是,CRLs 的 scope 并不一定需要和其 issuer 相关,当 CRLs 的 scope 超出其 issuer 所签发的证书时,这个 CRLs 就称为 indirect CRLs。甚至于,indirect CRLs 其实可以没有 issuer,这种情况使得可以在不动用 CA 私钥的情况下生成 CRLs。但是,很多客户端默认情况下不一定支持 indirect CRLs,所以并不常见。
具体可见 https://www.rfc-editor.org/rfc/rfc5280#page-55
https://youtu.be/8Vmv10p9Y44?si=1RFFOpoHqZwLfrY8
之前披露了 3M 和 Dupont 的黑料,这次来黑一把强生(Johnson & Johnson)。
多年以来,强生的爽身粉一直是美国家庭的必备品,也是安全和干爽的代名词,人们会将其用在任何地方,包括婴儿和成人。1999 年,部分家庭怀疑自己家人的癌症是因为强生公司生产的爽身粉中包含石棉,但是强生公司矢口否认,此案不了了之。
2018 年,路透社披露强生公司的内部文件显示,早在 1957 年强生就发现了其产品中包含石棉,并且有潜在的健康风险。1976 年 FDA 曾打算限制爽身粉中的石棉含量,但是强生公司的律师成功地说服了 FDA,假称爽身粉中不包含任何石棉,但实际上强生公司已经从多个实验室得知它的产品中石棉含量“相当高”。
这事儿还有另一个令人震惊的事实,强生在 1971 年为了测试石棉对人体的影响,聘用 Albert Kligman 从监狱(Philadelphia County Prison)中挑选了 50 名囚犯做活体实验,其中 44 人为黑人。在未告知风险的情况下,直接将石棉制品注射或涂抹到囚犯的皮肤上。如今我们知道石棉的致癌作用主要在肺部,所以当年的皮肤试验并未发现特别严重的副作用。此外,Kligman 声称自己并未违反当时的道德标准,至死也拒绝道歉。
* 路透社关于石棉和爽身粉的报道
* Bloomberg 关于监狱人体实验的报道
之前披露了 3M 和 Dupont 的黑料,这次来黑一把强生(Johnson & Johnson)。
多年以来,强生的爽身粉一直是美国家庭的必备品,也是安全和干爽的代名词,人们会将其用在任何地方,包括婴儿和成人。1999 年,部分家庭怀疑自己家人的癌症是因为强生公司生产的爽身粉中包含石棉,但是强生公司矢口否认,此案不了了之。
2018 年,路透社披露强生公司的内部文件显示,早在 1957 年强生就发现了其产品中包含石棉,并且有潜在的健康风险。1976 年 FDA 曾打算限制爽身粉中的石棉含量,但是强生公司的律师成功地说服了 FDA,假称爽身粉中不包含任何石棉,但实际上强生公司已经从多个实验室得知它的产品中石棉含量“相当高”。
这事儿还有另一个令人震惊的事实,强生在 1971 年为了测试石棉对人体的影响,聘用 Albert Kligman 从监狱(Philadelphia County Prison)中挑选了 50 名囚犯做活体实验,其中 44 人为黑人。在未告知风险的情况下,直接将石棉制品注射或涂抹到囚犯的皮肤上。如今我们知道石棉的致癌作用主要在肺部,所以当年的皮肤试验并未发现特别严重的副作用。此外,Kligman 声称自己并未违反当时的道德标准,至死也拒绝道歉。
* 路透社关于石棉和爽身粉的报道
* Bloomberg 关于监狱人体实验的报道
我此前对 AC 的理解存在一些偏差,Anonymous 最侧重保护的不是被签名的隐私数据(witness),而是数据拥有者(Holder)的身份。其应用场景是,当 Holder 为自己的 witness 提供 statement,Verifier 在验证这个 statement 的时候,也无法揭露 Holder 的身份。
拿传统的非对称签名来举个例子,会有三个角色:根证书持有者(Issuer),隐私数据拥有者(Holder),验证者(Verifier)。Holder 需要从 Issuer 获取自己的个人证书,用自己的私钥对 witness 进行签名生成 statement,然后将
(公钥证书链、statement、witness) 一起提交给 Verifier。Verifier 预先已信任了 Issuer 的根证书,从而验证了 Holder 的公钥可信,然后用 Holder 的公钥验证 statement,最终确认 witness 的真实性。为了提高隐私性,上述描述中有两个需要改进的需求:
1. 匿名性:Holder 的公钥证书暴露了自己的身份信息(attributes)
2. 零知识:Holder 为了验证向 Verifier 披露了 witness 的明文
这两个需求分别对应密码学的两个方向,前者是 anonymous credential,后者是 ZKP,分别有不同的协议家族和应用。虽然这两者的实现和应用很多时候互相交织,但是核心目的是不一样的。
以前我对 P ≠ NP 理解是有点偏感性的,以为就是描述只能被暴力搜索求解的问题是否能够被快速求解。
实际上 NP(Nondeterministic Polynomial time)这个词是描述了一类特殊的问题,这些问题的解可以被迅速证实,但是不能够被快速求解。
比如一副拼图,拼好后你可以短时间内验证拼图是否正确,最差情况下你挨个看一遍也足够了(多项式时间内)。但是没有一个简单的办法让你去从头完成一副拼图。P ≠ NP 描述的就是,能够在多项式时间内被证实的问题,是否也能够在多项式时间内被求解?
另一个经典的 NP 问题就是旅行家问题(Traveling Salesman Problem),找到一条路径,能够不重复地遍历所有的城市并回到起点。你可以很容易地验证某个路径的正确性,却很难找到这个路径。
不同的 NP 问题有不同的求解难度。其中最难的一些 NP 问题被称为 NP-completeness。这些最难的 NP 完备问题互相等价,预示着 NP 问题的一些核心本质,一旦有任何一个 NP 完备问题被破解,就意味着所有的 NP 问题都能被迅速求解。
密码学里经常看到 Random Oracle Model 这个名字。这是一种假想中的完美 Hash Function,具有如下特性:
1. 接收一个从未见过的输入,返回一个唯一且不可预测的输出。
2. 接收一个曾经见过的输入,返回和上次相同的输出。
ROM 这样的完美 Hash Function 在现实中并不存在,但是现实中的 Hash 都是在尽可能的接近它。经常举的一个例子就是 SHA-1,它不是 ROM 的原因就是有 length extention attack 的风险。
假设有一个消息
1. 接收一个从未见过的输入,返回一个唯一且不可预测的输出。
2. 接收一个曾经见过的输入,返回和上次相同的输出。
ROM 这样的完美 Hash Function 在现实中并不存在,但是现实中的 Hash 都是在尽可能的接近它。经常举的一个例子就是 SHA-1,它不是 ROM 的原因就是有 length extention attack 的风险。
假设有一个消息
m,H = SHA1(m)。如果已知 H 和 m 的长度,那么就可以伪造 H' = SHA1(m || m')。也就是说,即使不知道 m,我也可以计算出 m + m' 的哈希值。这就违背了 ROM 不可预测性的原则。我一直是 macbook air 的鼓吹者,推荐利用 macbook air 作为随身移动办公的 GUI,然后远程连接性能强大且廉价的 PC 服务器。而 tailscale 则充当网络的连通者。
拿我自己来说,我家里有一台不关机的 windows PC,作为我的主力娱乐机。上面通过 vmware player 运行了一台 linux 服务器作为我的主力开发机。然后随身携带一台 macbook air 作为我的移动办公机。
mba 轻便,UI 友好,而且没有风扇不会积灰,Apple Silicon 的性能足够强大。因为负载都在远程,本地极为节能,续航时间超长。
有越来越多的人对 tailscale 感兴趣,我整理了一下以前的笔记:
1. 关于 tailscale 的安装与配置 https://blog.laisky.com/p/tailscale/
2. 关于 tailscale 的网络穿透 https://blog.laisky.com/p/tailscale-nat/
Vmware Pro 个人用户免费啦! https://blogs.vmware.com/workstation/2024/05/vmware-workstation-pro-now-available-free-for-personal-use.html
拿我自己来说,我家里有一台不关机的 windows PC,作为我的主力娱乐机。上面通过 vmware player 运行了一台 linux 服务器作为我的主力开发机。然后随身携带一台 macbook air 作为我的移动办公机。
mba 轻便,UI 友好,而且没有风扇不会积灰,Apple Silicon 的性能足够强大。因为负载都在远程,本地极为节能,续航时间超长。
有越来越多的人对 tailscale 感兴趣,我整理了一下以前的笔记:
1. 关于 tailscale 的安装与配置 https://blog.laisky.com/p/tailscale/
2. 关于 tailscale 的网络穿透 https://blog.laisky.com/p/tailscale-nat/
Vmware Pro 个人用户免费啦! https://blogs.vmware.com/workstation/2024/05/vmware-workstation-pro-now-available-free-for-personal-use.html
openai 套皮站的相关信息另建了一个 channel,发布更新信息,就不再在这里发了。这个频道还是专注做有价值信息的笔记,这是最后一条了。
套皮站支持了 claude 1、2、3: https://t.me/laisky_oai/5
套皮站支持了 claude 1、2、3: https://t.me/laisky_oai/5
前文介绍了 ECC 和 ECDH。本来想接着写一篇 ECDSA 和 Schnorr Signature 的笔记的,但是内容有点长,干脆写了篇博客,介绍 ECC、ECDH、ECDSA、Schnorr、MuSig。 #crypto
https://blog.laisky.com/p/ecc/
https://blog.laisky.com/p/ecc/
首先,绘制一个扭曲的曲线。然后在这个曲线上定义一种名为加法的运算:
1. P 点和 Q 点相加: 绘制直线 PQ,得到和曲线的第三交点为 R,R 的 x 轴镜像点为结果。
2. P 点自己和自己相加: 绘制 P 点的切线,得到和曲线的交点 R,其镜像点为结果。
3. 定义零值为 y 轴的无穷远处,和零相加等于画一条垂直线。
如上我们定义了运算规则,接下来就是从曲线的点中选取一些点构成一个循环群。群就是一组满足相同规律的数的集合。循环群(cycle group)中存在一些本原元(primitive element),这些原元通过不断累加,可以遍历整个群。
形象地说,你找到一个本原元点(primitive element),然后不断地累加这个点,利用前文我们所介绍的加法运算,你其实就是在曲线上不断地跳跃,并最终会跳回起点。
ECC 加密算法中,就是构建这么一个曲线,它的循环群内的成员数量达到 2^100 次方,我们认为这个量级的数是无法靠暴力遍历破解的。这个曲线的每一个值是根据一个大素数的模的方程构建的,成员数量约等于这个素数的位数,一个 160-bits 的素数可以构建一个包含 2^160 个点的群。
然后给出这么一个公式
dP = T。P 是一个 primitive element,它累加 d 次后会得到 T 点。P、T 是公钥,d 是私钥。这也是为什么 ECC 的私钥可以很短。也就是说,我公开展示最终的 T 点,但是不告诉你我跳跃了多少次。你是难以通过暴力遍历去求解 d 的。这个
dP = T 就是构建了一个离散对数问题(DLP),计算 dP 很简单,但是逆运算求算 d 很复杂,需要暴力搜索 2^100 的空间。既然利用 ECC 构建了 DLP,那么就可以利用 ECC 替换传统 DLP 问题,比如 Diffie-Hellman 密钥交换算法,现在可以重构为基于 ECC 的 ECDH 算法。
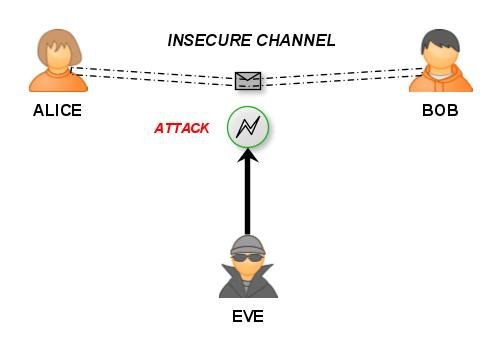
Alice 和 Bob 都确认一个曲线和一个 primitive element P。然后双方各自生成一个 d,然后交换计算结果 dP。拿到对方的 dP 后再乘上自己的 d,就会得到一个相同的 T。窃听者能拿到曲线、P、d_alice*P 和 d_bob*P,但是他无法逆向求解 d_alice 和 d_bob,所以无法破解最终的 T。
PS: 所有的 DHKX 算法,都难以防御中间人攻击(MITM attack),即攻击者可以篡改通信,同时和双方握手。解决办法是引入数字证书,对对方的公钥进行签名。
PS: 安全的椭圆曲线是很难绘制的,一般参考 NIST 的推荐。 #crypto
next: https://t.me/laiskynotes/173
https://youtu.be/r0Ji7KqqEqg?si=Dobd3qPl8BW8zZHm Hostomel 之战的详细解释。实际上俄军 VDV 强袭机场得手后,当天下午就被包围了。乌军的炮击破坏了机场设施,使得 18 架次的后续增援部队无法降落。
我觉得降落了估计也不会有特别大的影响,毕竟俄军主力很快就从北方推进到了此处,然而除了搞个 bucha 大屠杀外再也无所作为。
我觉得降落了估计也不会有特别大的影响,毕竟俄军主力很快就从北方推进到了此处,然而除了搞个 bucha 大屠杀外再也无所作为。
想象这么一个场景,政府给你签发了身份证,政府为这个证件背书上面的信息都是真实有效的。
然后你为了上某 X 网站,需要证明你已经年满 18 岁。于是你把身份证信息加密后上传给网站,然后选择只披露其中的姓名和年龄属性。网站通过签名验证这个身份信息确实是由政府颁发的,其中的信息真实可靠,而且证件上的年龄显示你已经年满 18 岁,而证件上的其他信息都对网站不可见。
在上述流程中,政府(issuer)为你(holder)签发了信息,你选择将部分信息披露给网站(verifier)。这就是 Anonymous Credential(Anoncred)或称为 Attribute-based Credential(ABC)。
这一算法的特点包括:
1. issuer 可以使用一对公私钥,签发 K 组信息。
2. holder 可以选择性地披露 N 组信息(N<=K)。
3. verifier 可以通过 issuer 的公钥验证 holder 所披露的信息的有效性。
穿插提一下密码学中的 Commitment Schema。Alice 可以对一个未披露的 Message 声明 Commitment,Bob 可以保留这一 Commitment,直到 Alice 披露 Message 后,Bob 可以验证这一 Message 是否与 Commitment 一致。结合前面所提的 ABC,其实就是一个 Commitment Schema,Issuer 为 Holder 的信息背书(statement signature),Verifier 需要 Holder 披露信息后才能验证真实性。
最简单的实现就是基于 RSA 的 CL Signature,更多细节可点击查看: https://telegra.ph/CL-Signature-02-26-2 #crypto
next:
- ECC & ECDSA & ECDH
- AC & ZKP